Skip to content

Rigid-body Motion

Rigid-body Motion Representation

Notes in this section are mainly based on reference [1] and follow the same notations.

Notations

A superscript is used to denote the reference frame, for example

  • The position of point 0 with respect to b frame: \(p^b_0\)
  • The orientation of the body frame b with respect to the world frame w: \(R^w_b\)

Rigid Motion

"A rigid motion is an ordered pair \((d, R)\) where \(d \in \mathcal{R}^3\) and \(R \in \mathcal{SO}(3)\). The group of all rigid motions is known as the Special Euclidean Group and is denoted by \(\mathcal{SE}(3)\)." [1]

\[ \mathcal{SE}(3) = \mathcal{R}(3) \times \mathcal{SO}(3) \]

The \(d\) part corresponds to a translation and the \(R\) part corresponds to a rotation.

Position Representation

A position vector can be represented with a column vector. A point in space can be represented with different coordinates when the representations are with respect to different reference frames. For example, a point on a 2D plane can be represented as

\[ p^0 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}, \;\;\; p^1 = \begin{bmatrix} \sqrt{2} \\ 0 \end{bmatrix} \]

where reference frame 1 is rotated counter-clockwise by \(45^{\circ}\) with respect to reference frame 0.

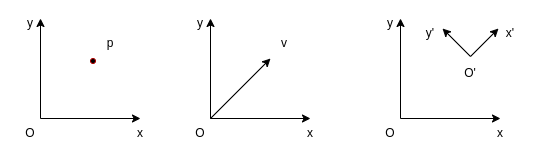
Note that a column vector on the other hand may be the representation of different objects, not limited to a point:

  1. The position of a point
  2. The coordinates of a free vector, representing a translation
  3. The position of one coordinate system with respect to another

Rotation Representation

Rotation Matrix

A rotation is most commonly represented with a rotation matrix \(R \in \mathcal{SO}(n)\), where \(\mathcal{SO}(n)\) denotes the Special Orthogonal group of order n.

The properties of a rotation matrix \(R\):

  • \(R \in \mathcal{SO}(n)\)
  • \(R^{-1} \in \mathcal{SO}(n)\)
  • \(R^{-1} = R^T\)
  • The columns (and therefore the rows) of \(R\) are mutually orthogonal
  • Each column (and therefore each row) of \(R\) is a unit vector
  • \(\det{R} = 1\)

The rotation matrix on a 2D plane is given as

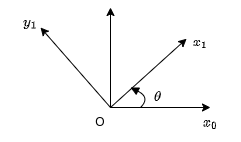
\[ R^0_1 = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}, \;\;\; R^1_0 = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \]

Thus for a point \(p^{0} = \begin{bmatrix} 1 \\ 1\end{bmatrix}\) in reference frame 0, it can be represented with respect to reference frame 1

\[ p^{1} = R^1_0p^0 = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} 1 \\ 1\end{bmatrix} = \begin{bmatrix} \cos\theta + \sin\theta \\ -sin\theta+\cos\theta\end{bmatrix} \]

In the case that \(\theta=\pi/4\), we get \(p^1=\begin{bmatrix} \sqrt{2} \\ 0\end{bmatrix}\), which is the same with the example given above.

A rotation matrix can also be interpreted in multiple ways [1]:

  1. A coordinate transformation relating the coordinates of a point \(p\) in two different frames
  2. The orientation of a transformed coordinate frame with respect to a fixed coordinate frame
  3. An operator taking a vector and rotating it to a new vector in the same coordinate system

Note that applying a translation to a free vector won't change the vector (direction and magnitude), but applying a rotation may change the vector to be a new one.

Euler Angles

A rotation matrix can be specified by the composition of 3 consecutive rotations. Each of the rotation is represented by an angle (\(\psi/\theta/\phi\)) around a specified main axis (\(x/y/z\)). There are many different combinations of Euler angles. For example, an ZYZ-Euler angle is given by \(R_j{ZYZ} = R_{z,\phi}R_{y,\theta}R_{z,\psi}\).

Roll, Pitch, Yaw Angles

Roll, pitch, yaw angles can be seen as a special case of Euler angles. In robotics, the body coordinate frame fixed to the robot is usually defined as z-axis pointing up, x-axis pointing front and y-axis point left. In such a case, yaw angle cooresponds to the rotation around z-axis, pitch angle cooresponds to the rotation around y-axis and roll angle cooresponds to the rotation around x-axis. Note that different conventions do exist for defining the body reference frame and naming roll, pitch and yaw angles (e.g. in aerospace engineering literature).

Axis/Angle

Axis/angle representation used the rotation angle around an arbitrary axis to represent a rotation and is often used to create other types of representations.

Quaternion

Quaternion representation is widely used for computation of 3D rotations. It is given in the form

\[ \vec{q} = w + x\vec{i} + y\vec{j} + z\vec{k}, \textnormal{or}\;\; \vec{q} = (w,x,y,z) = (w, \vec{v}) \]

The basis \(\vec{i},\vec{j},\vec{k}\) follow the following rules:

\[ \begin{align*} ij &= -ji = k \\ jk &= -kj = i \\ ki &= -ik = j \\ i^2 = j^2 &= k^2 = ijk = -1 \end{align*} \]

Generally the quaternions we use to describe orientations are unit quaternions, i.e. \(\| q \| = \sqrt{w^2 + x^2 + y^2 + z^2} = 1\). A non-unit quaternion can be normalized by

\[ \hat{q} = \frac{q}{\| q \|} \]

Note that "matrices represent linear transforms; quaternions represent a special case of linear transform: rotations in 3 dimensions"[4].

In addition to the quaternion itself, we have:

  • Quaternion Conjugate: \(q^{*} = (w, -\vec{v})\). Geometrically, the conjugate represents the inverse of the rotation that q represents. If q rotates a vector in 3D space in one direction, \(q^{*}\) rotates it back to the original position. In terms of rotation, if q rotates a coordinate frame from frame A to frame B, then \(q^{*}\) rotates it from frame B back to frame A.
  • The negative of a quaternion q, denoted as \(-q\), is simply the quaternion with all the components negated: \(q^{*} = (-w, -\vec{v})\). Geometrically, a quaternion and its negative represent the same rotation in 3D space. This is because a quaternion and its negative point to the same point on the 4D unit sphere, which corresponds to the same rotation in 3D space.
  • Quaternion Inverse: \(q^{-1} = \frac{q^{*}}{{\| q \|}^2}\), for unit quaternion, we have \(q^{*} = q^{-1}\)

The following operations are frequently used:

  • A point or vector \(\vec{v}\) can be rotated by a quaternion \(q\) by operation
\[ \vec{v}^{\prime} = q\vec{v}q^{-1} \]
  • An orientation \(O\) can be rotated by a quaterion \(q\) by operation
\[ O^{\prime} = qO \]
  • Multiple rotations can be composed by multiply the quatenion from the left (pre-multiply), for example, \(O^\prime\) is the orientation as if \(q_1\) were applied to \(O\), then \(q_2\), then \(q_3\)
\[ O^{\prime} = q_3q_2q_1O \]

Quaternions can be used to do the calculation efficiently but are not so intuitive to understand. Reference [3] and [5] are highly recommended if more details are required.

Composition of Rotations

A summary of the rule of composition of rotational transformations can be found in [1]:

Given a fixed frame \(o_0x_0y_0z_0\), a current frame \(o_1x_1y_1z_1\), together with rotation matrix \(R^0_1\) relating them,

  • if a third frame \(o_2x_2y_2z_2\) is obtained by a rotation \(R\) performed relative to the current frame then post-multiply \(R^0_1\) by \(R=R^1_2\) to obtain
\[R^0_2 = R^0_1R^1_2\]
  • if the second rotation is to be performed relative to the fixed frame, then pre-multiply \(R^0_1\) by \(R\) to obtain
\[R^0_2 = RR^0_1\]

The first case of composition is more commonly seen and it's also more intuitive to understand.

The multiple meanings of a vector and matrix

The multiple meanings a vector or a matrix can easily cause confusions when handling rigid-body motions. Interpretation 3 of a vector and interpretation 2 of a matrix listed above are often used when you're considering the relationship between two cooredinate frames in order to set up new frames. Interpretation 2 of a vector and interpretation 3 of a matrix are often used when you're handling the calculation of transformations in order to transform a pose from one coordinate frame to another.

Homogeneous Transformation

A homogeneous transformation matrix combines translation and rotation into one matrix and could be used to simplify the calculation of transformations.

\[ H = \begin{bmatrix} R & d \\ 0 & 1 \end{bmatrix}; \;\;\; R \in \mathcal{SO}(3), d \in \mathcal{R}^3 \]

Using the factor that \(R\) is orthogonal, we can get the inverse transformation as

\[ H^{-1} = \begin{bmatrix} R^T & -R^Td \\ 0 & 1 \end{bmatrix} \]

In order to apply a homogeneous transformation, a column vector must be augmented

\[ P^0 = \begin{bmatrix} p^0 \\ 1 \end{bmatrix}, P^1 = \begin{bmatrix} p^1 \\ 1 \end{bmatrix} \]

Then we have the equivalent calculation with

\[p^0 = R^0_1p^1 + d^0_1\]

in the matrix form

\[ P^0 = H^0_1P^1 \]

Composition rule for homogeneous transformations

Given a homogeneous transformation \(H^0_1\) relating two frames [1]:

  • if a second rigid motion, represented by \(H \in \mathcal{SE}(3)\) is performed to the current frame, then
\[ H^0_2 = H^0_1H^1_2 \]
  • if the second rigid motion is performed relative to the fixed frame, then
\[ H^0_2 = HH^0_1 \]

Rigid-body Motion Calculation with Eigen

More relevant details can be found from Eigen offical documentation page [6][7][8] and this tutorial [9]. Here I only keep the most frequently used use cases. Source code in this section can be found on this GitHub repo.

Basic Operations of Matrices/Vectors

// matrix transpose and inverse
Eigen::MatrixXd R(3, 3);
R << 1, 2, 1,
    2, 3, 4,
    3, 1, 5;

// element access
// note: matrix index (row, column), index starts from 0
std::cout << "R(0,0) = " << R(0, 0) << std::endl;
std::cout << "R(1,2) = " << R(1, 2) << std::endl;
std::cout << "R(2,2) = " << R(2, 2) << std::endl;

Eigen::MatrixXd R_block = R.block(1, 1, 2, 2);
std::cout << "Take sub-matrix: \n" << R_block << std::endl;

Eigen::MatrixXd R_row = R.row(1);
std::cout << "Take row: \n" << R_row << std::endl;

Eigen::MatrixXd R_col = R.col(0);
std::cout << "Take column: \n" << R_col << std::endl;

// multiplication
Eigen::Matrix3d R2 = Eigen::Matrix3d::Identity();
auto R3 = R * R2;
std::cout << "R * R2: \n" << R3 << std::endl;

// transpose and inverse
Eigen::MatrixXd R_transpose = R.transpose();
Eigen::MatrixXd R_inverse = R.inverse();

std::cout << "R: \n" << R << std::endl;
std::cout << "R_transpose: \n" << R_transpose << std::endl;
std::cout << "R_inverse: \n" << R_inverse << std::endl;

// dot product and cross product:
Eigen::Vector3d v(1, 2, 3);
Eigen::Vector3d w(0, 1, 2);

double v_dot_w = v.dot(w);
Eigen::Vector3d v_cross_w = v.cross(w);

std::cout << "v: \n" << v << std::endl;
std::cout << "w: \n" << w << std::endl;
std::cout << "v_dot_w: \n" << v_dot_w << std::endl;
std::cout << "v_cross_w: \n" << v_cross_w << std::endl;

Pose Representation with Eigen

The type "Vector3f" is a column vector in Eigen, thus it can be used directly to represent a position. Eigen also provides data types to present a rotation matrix, axis-angle and quaternion.

Examples for the pose (position and orientation) representation with Eigen:

Eigen::Vector2d p2d(1.0, 2.0);
std::cout << "A point in 2d: \n" << p2d << std::endl;

Eigen::Vector3d p3d(1.0, 2.0, 3.0);
std::cout << "A point in 3d: \n" << p3d << std::endl;

Eigen::Matrix3d R;
R << 0, -1, 0, 1, 0, 0, 0, 0, 1;
std::cout << "A rotation matrix: \n" << R << std::endl;

Eigen::Quaterniond q_from_R(R);
std::cout << "A quaternion from rotation matrix: \n" << q_from_R.coeffs() << std::endl;

Eigen::Quaterniond q_unit = Eigen::Quaterniond::Identity();
std::cout << "A unit quaternion: \n" << q_unit.coeffs() << std::endl;

Eigen::Quaterniond q(2, 0, 1, -3);
std::cout << "A non-normalized quaternion: \n" << q.coeffs() << std::endl;

q.normalize();
std::cout << "A normalized quaternion: \n" << q.w() << std::endl << q.vec() << std::endl;

Eigen::Matrix3d R_from_q = q.toRotationMatrix();
std::cout << "A rotation matrix from quaternion: \n" << R_from_q << std::endl;

Eigen::Matrix3f R_from_angleaxis;
R_from_angleaxis = Eigen::AngleAxisf(0.25 * M_PI, Eigen::Vector3f::UnitX())
    * Eigen::AngleAxisf(0.5 * M_PI, Eigen::Vector3f::UnitY())
    * Eigen::AngleAxisf(0.33 * M_PI, Eigen::Vector3f::UnitZ());
std::cout << "A rotation matrix from angle-axis: \n" << R_from_angleaxis << std::endl;

Eigen::Quaternionf q_from_angleaxis(Eigen::AngleAxisf(0.33 * M_PI, Eigen::Vector3f::UnitZ()));
std::cout << "A quaternion from angle-axis: \n" << q_from_angleaxis.coeffs() << std::endl;

Transformation with Eigen

Reference

  • [1] Spong, M.W. and Hutchinson, S. and Vidyasagar, M. (2005). Robot Modeling and Control. Wiley.
  • [2] Lynch, K. M., & Park, F. C. (2017). Modern Robotics: Mechanics, Planning, and Control. Cambridge Univeristy Press.
  • [3] https://eater.net/quaternions
  • [4] https://www.anyleaf.org/blog/quaternions:-a-practical-guide
  • [5] https://www.3dgep.com/understanding-quaternions/
  • [6] https://eigen.tuxfamily.org/dox/group__QuickRefPage.html
  • [7] https://eigen.tuxfamily.org/dox/group__TutorialGeometry.html
  • [8] https://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html
  • [9] https://www.cc.gatech.edu/classes/AY2015/cs4496_spring/Eigen.html